Chapter 5 Clustering

5.1 Overview

Clustering is an unsupervised learning procedure that is used to empirically define groups of cells with similar expression profiles. Its primary purpose is to summarize complex scRNA-seq data into a digestible format for human interpretation. This allows us to describe population heterogeneity in terms of discrete labels that are easily understood, rather than attempting to comprehend the high-dimensional manifold on which the cells truly reside. After annotation based on marker genes, the clusters can be treated as proxies for more abstract biological concepts such as cell types or states.

At this point, it is helpful to realize that clustering, like a microscope, is simply a tool to explore the data. We can zoom in and out by changing the resolution of the clustering parameters, and we can experiment with different clustering algorithms to obtain alternative perspectives of the data. This iterative approach is entirely permissible given that data exploration constitutes the majority of the scRNA-seq data analysis workflow. As such, questions about the “correctness” of the clusters or the “true” number of clusters are usually meaningless. We can define as many clusters as we like, with whatever algorithm we like - each clustering will represent its own partitioning of the high-dimensional expression space, and is as “real” as any other clustering.

A more relevant question is “how well do the clusters approximate the cell types or states of interest?” Unfortunately, this is difficult to answer given the context-dependent interpretation of the underlying biology. Some analysts will be satisfied with resolution of the major cell types; other analysts may want resolution of subtypes; and others still may require resolution of different states (e.g., metabolic activity, stress) within those subtypes. Moreover, two clusterings can be highly inconsistent yet both valid, simply partitioning the cells based on different aspects of biology. Indeed, asking for an unqualified “best” clustering is akin to asking for the best magnification on a microscope without any context.

Regardless of the exact method used, clustering is a critical step for extracting biological insights from scRNA-seq data. Here, we demonstrate the application of several commonly used methods with the 10X PBMC dataset.

## class: SingleCellExperiment 
## dim: 33694 3985 
## metadata(1): Samples
## assays(2): counts logcounts
## rownames(33694): RP11-34P13.3 FAM138A ... AC213203.1 FAM231B
## rowData names(2): ID Symbol
## colnames(3985): AAACCTGAGAAGGCCT-1 AAACCTGAGACAGACC-1 ...
##   TTTGTCAGTTAAGACA-1 TTTGTCATCCCAAGAT-1
## colData names(3): Sample Barcode sizeFactor
## reducedDimNames(3): PCA TSNE UMAP
## mainExpName: NULL
## altExpNames(0):

5.2 Graph-based clustering

5.2.1 Background

Popularized by its use in Seurat, graph-based clustering is a flexible and scalable technique for clustering large scRNA-seq datasets. We first build a graph where each node is a cell that is connected to its nearest neighbors in the high-dimensional space. Edges are weighted based on the similarity between the cells involved, with higher weight given to cells that are more closely related. We then apply algorithms to identify “communities” of cells that are more connected to cells in the same community than they are to cells of different communities. Each community represents a cluster that we can use for downstream interpretation.

The major advantage of graph-based clustering lies in its scalability. It only requires a \(k\)-nearest neighbor search that can be done in log-linear time on average, in contrast to hierachical clustering methods with runtimes that are quadratic with respect to the number of cells. Graph construction avoids making strong assumptions about the shape of the clusters or the distribution of cells within each cluster, compared to other methods like \(k\)-means (that favor spherical clusters) or Gaussian mixture models (that require normality). From a practical perspective, each cell is forcibly connected to a minimum number of neighboring cells, which reduces the risk of generating many uninformative clusters consisting of one or two outlier cells.

The main drawback of graph-based methods is that, after graph construction, no information is retained about relationships beyond the neighboring cells1. This has some practical consequences in datasets that exhibit differences in cell density, as more steps through the graph are required to move the same distance through a region of higher cell density. From the perspective of community detection algorithms, this effect “inflates” the high-density regions such that any internal substructure or noise is more likely to cause formation of subclusters. The resolution of clustering thus becomes dependent on the density of cells, which can occasionally be misleading if it overstates the heterogeneity in the data.

5.2.2 Implementation

To demonstrate, we use the clusterCells() function in scran on PBMC dataset. All calculations are performed using the top PCs to take advantage of data compression and denoising. This function returns a vector containing cluster assignments for each cell in our SingleCellExperiment object.

## nn.clusters
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16 
## 205 508 541  56 374 125  46 432 302 867  47 155 166  61  84  16

We assign the cluster assignments back into our SingleCellExperiment object as a factor in the column metadata. This allows us to conveniently visualize the distribution of clusters in a \(t\)-SNE plot (Figure 5.1).

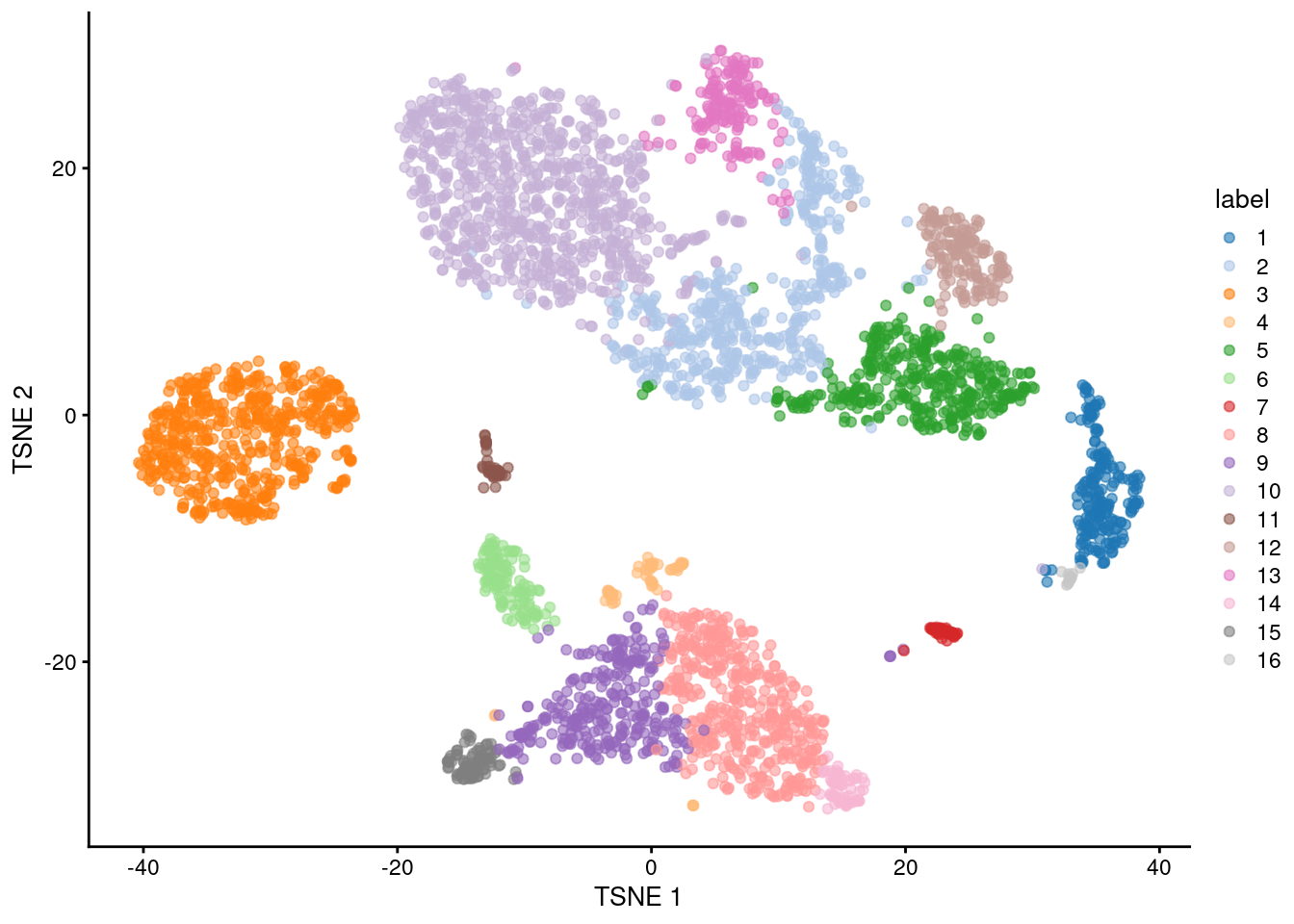
$t$-SNE plot of the 10X PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from graph-based clustering.

Figure 5.1: \(t\)-SNE plot of the 10X PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from graph-based clustering.

By default, clusterCells() uses the 10 nearest neighbors of each cell to construct a shared nearest neighbor graph. Two cells are connected by an edge if any of their nearest neighbors are shared, with the edge weight defined from the highest average rank of the shared neighbors (Xu and Su 2015). The Walktrap method from the igraph package is then used to identify communities.

If we wanted to explicitly specify all of these parameters, we would use the more verbose call below. This uses a SNNGraphParam object from the bluster package to instruct clusterCells() to detect communities from a shared nearest-neighbor graph with the specified parameters. The appeal of this interface is that it allows us to easily switch to a different clustering algorithm by simply changing the BLUSPARAM= argument, as we will demonstrate later in the chapter.

## nn.clusters2
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16 
## 205 508 541  56 374 125  46 432 302 867  47 155 166  61  84  16

We can also obtain the graph itself by specifying full=TRUE in the clusterCells() call. Doing so will return all intermediate structures that are used during clustering, including a graph object from the igraph package. This graph can be visualized using a force-directed layout (Figure 5.2), closely related to \(t\)-SNE and UMAP, though which of these is the most aesthetically pleasing is left to the eye of the beholder.

## IGRAPH beb117a U-W- 3985 133130 -- 
## + attr: weight (e/n)
## + edges from beb117a:
##  [1] 1--  21 1--  65 1-- 136 1-- 223 1-- 394 1-- 398 1-- 517 1-- 527 1-- 552
## [10] 1-- 657 1-- 662 1-- 807 1-- 847 1-- 880 1-- 924 1-- 929 1-- 988 1--1022
## [19] 1--1038 1--1048 1--1151 1--1168 1--1302 1--1356 1--1548 1--1569 1--1631
## [28] 1--1679 1--1779 1--1829 1--1860 1--1864 1--1899 1--1908 1--1912 1--2051
## [37] 1--2114 1--2134 1--2197 1--2204 1--2246 1--2312 1--2375 1--2522 1--2553
## [46] 1--2748 1--2872 1--2904 1--2916 1--3087 1--3209 1--3368 1--3372 1--3622
## [55] 1--3647 1--3682 1--3685 1--3694 1--3724 1--3745 1--3765 1--3854 1--3875
## [64] 1--3952 1--3960 1--3962 1--3977 1--3985 2--  25 2--  33 2--  47 2-- 138
## + ... omitted several edges
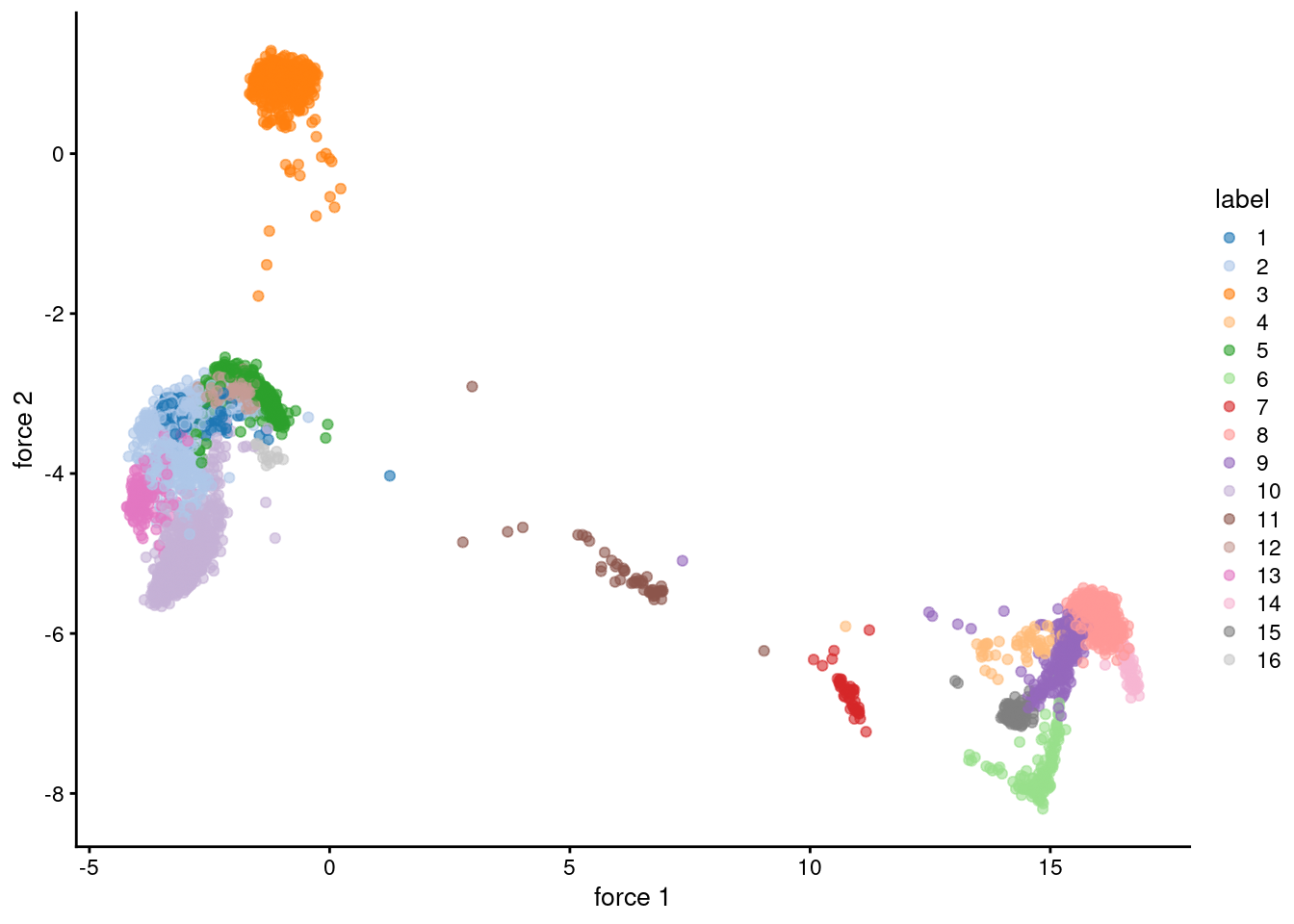
Force-directed layout for the shared nearest-neighbor graph of the PBMC dataset. Each point represents a cell and is coloured according to its assigned cluster identity.

Figure 5.2: Force-directed layout for the shared nearest-neighbor graph of the PBMC dataset. Each point represents a cell and is coloured according to its assigned cluster identity.

In addition, the graph can be used to generate detailed diagnostics on the behavior of the graph-based clustering (link("graph-diagnostics", "OSCA.advanced")).

5.2.3 Adjusting the parameters

A graph-based clustering method has several key parameters:

  • How many neighbors are considered when constructing the graph.
  • What scheme is used to weight the edges.
  • Which community detection algorithm is used to define the clusters.

One of the most important parameters is k, the number of nearest neighbors used to construct the graph. This controls the resolution of the clustering where higher k yields a more inter-connected graph and broader clusters. Users can exploit this by experimenting with different values of k to obtain a satisfactory resolution.

## clust.5
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20 
## 523 302 125  45 172 573 249 439 293  95 772 142  38  18  62  38  30  16  15   9 
##  21  22 
##  16  13
## clust.50
##   1   2   3   4   5   6   7   8   9  10 
## 869 514 194 478 539 944 138 175  89  45

Further tweaking can be performed by changing the edge weighting scheme during graph construction. Setting type="number" will weight edges based on the number of nearest neighbors that are shared between two cells. Similarly, type="jaccard" will weight edges according to the Jaccard index of the two sets of neighbors. We can also disable weighting altogether by using a simple \(k\)-nearest neighbor graph, which is occasionally useful for downstream graph operations that do not support weights.

## clust.num
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19 
## 199 541 354 294 458 123  47  45 170 397 838 150  40  80 136  50  31  16  16
## clust.jaccard
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17 
## 201 541 740 233 352  47 124 841  45 361  40 154  80  61 133  16  16
## clust.none
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16 
## 541 446  54 170 699  45 126 172 128 907 286  47 158 137  54  15

The community detection can be performed by using any of the algorithms provided by igraph. We have already mentioned the Walktrap approach, but many others are available to choose from:

It is straightforward to compare two clustering strategies to see how they differ (link("comparing-different-clusterings", "OSCA.advanced")). For example, Figure 5.3 suggests that Infomap yields finer clusters than Walktrap while fast-greedy yields coarser clusters.

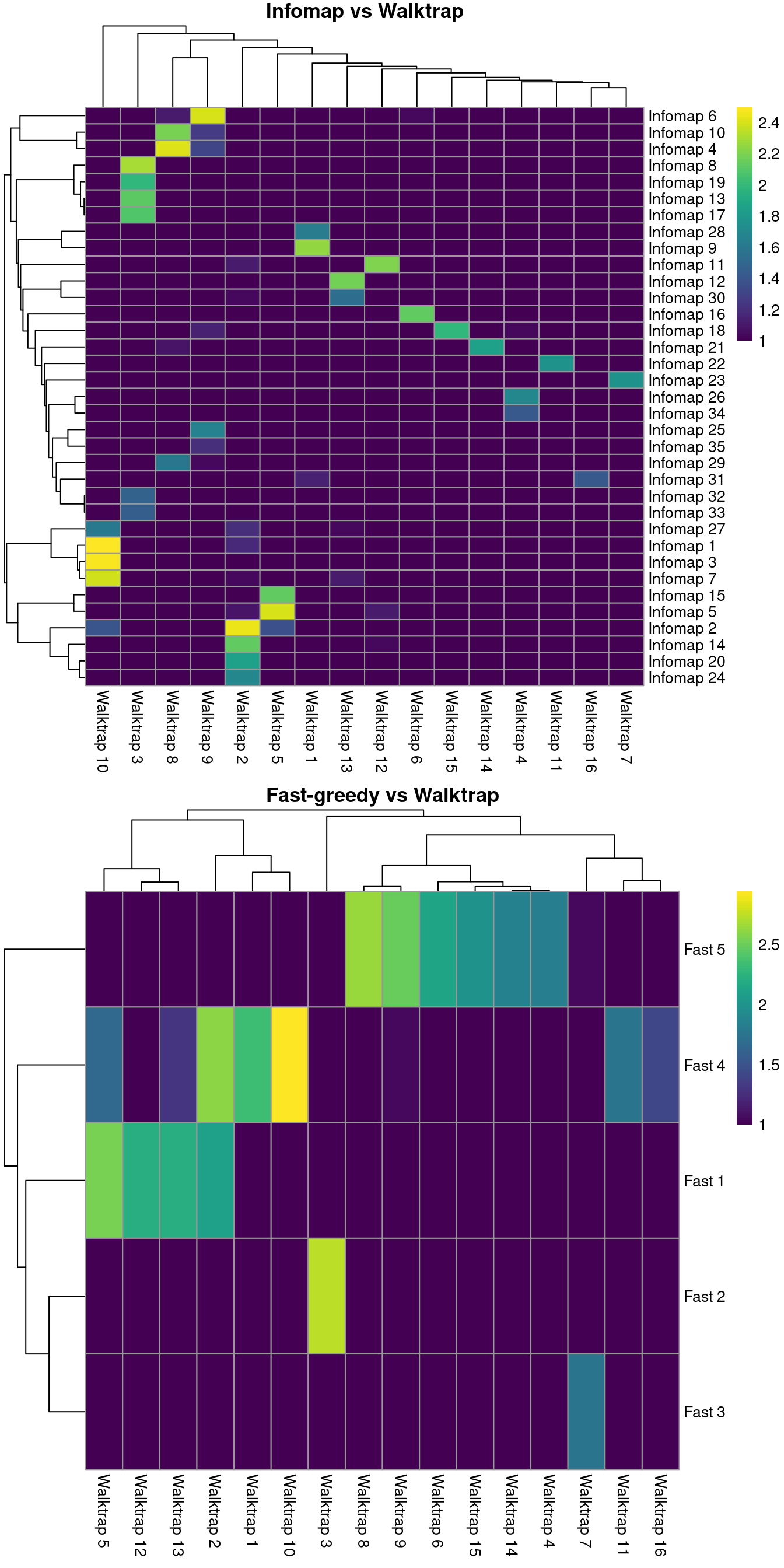
Number of cells assigned to combinations of cluster labels with different community detection algorithms in the PBMC dataset. Each entry of each heatmap represents a pair of labels, coloured proportionally to the log-number of cells with those labels.

Figure 5.3: Number of cells assigned to combinations of cluster labels with different community detection algorithms in the PBMC dataset. Each entry of each heatmap represents a pair of labels, coloured proportionally to the log-number of cells with those labels.

Pipelines involving scran default to rank-based weights followed by Walktrap clustering. In contrast, Seurat uses Jaccard-based weights followed by Louvain clustering. Both of these strategies work well, and it is likely that the same could be said for many other combinations of weighting schemes and community detection algorithms.

5.3 Vector quantization with \(k\)-means

5.3.1 Background

Vector quantization partitions observations into groups where each group is associated with a representative point, i.e., vector in the coordinate space. This is a type of clustering that primarily aims to compress data by replacing many points with a single representative. The representatives can then be treated as “samples” for further analysis, reducing the number of samples and computational work in later steps like, e.g., trajectory reconstruction (Ji and Ji 2016). This approach will also eliminate differences in cell density across the expression space, ensuring that the most abundant cell type does not dominate downstream results.

\(k\)-means clustering is a classic vector quantization technique that divides cells into \(k\) clusters. Each cell is assigned to the cluster with the closest centroid, which is done by minimizing the within-cluster sum of squares using a random starting configuration for the \(k\) centroids. We usually set \(k\) to a large value such as the square root of the number of cells to obtain fine-grained clusters. These are not meant to be interpreted directly, but rather, the centroids are used in downstream steps for faster computation. The main advantage of this approach lies in its speed, given the simplicity and ease of implementation of the algorithm.

5.3.2 Implementation

We supply a KmeansParam object in clusterCells() to perform \(k\)-means clustering with the specified number of clusters in centers=. We again use our top PCs after setting the random seed to ensure that the results are reproducible. In general, the \(k\)-means clusters correspond to the visual clusters on the \(t\)-SNE plot in Figure 5.4, though there are some divergences that are not observed in, say, Figure 5.1. (This is at least partially due to the fact that \(t\)-SNE is itself graph-based and so will naturally agree more with a graph-based clustering strategy.)

## clust.kmeans
##   1   2   3   4   5   6   7   8   9  10 
## 548  46 408 270 539 199 148 783 163 881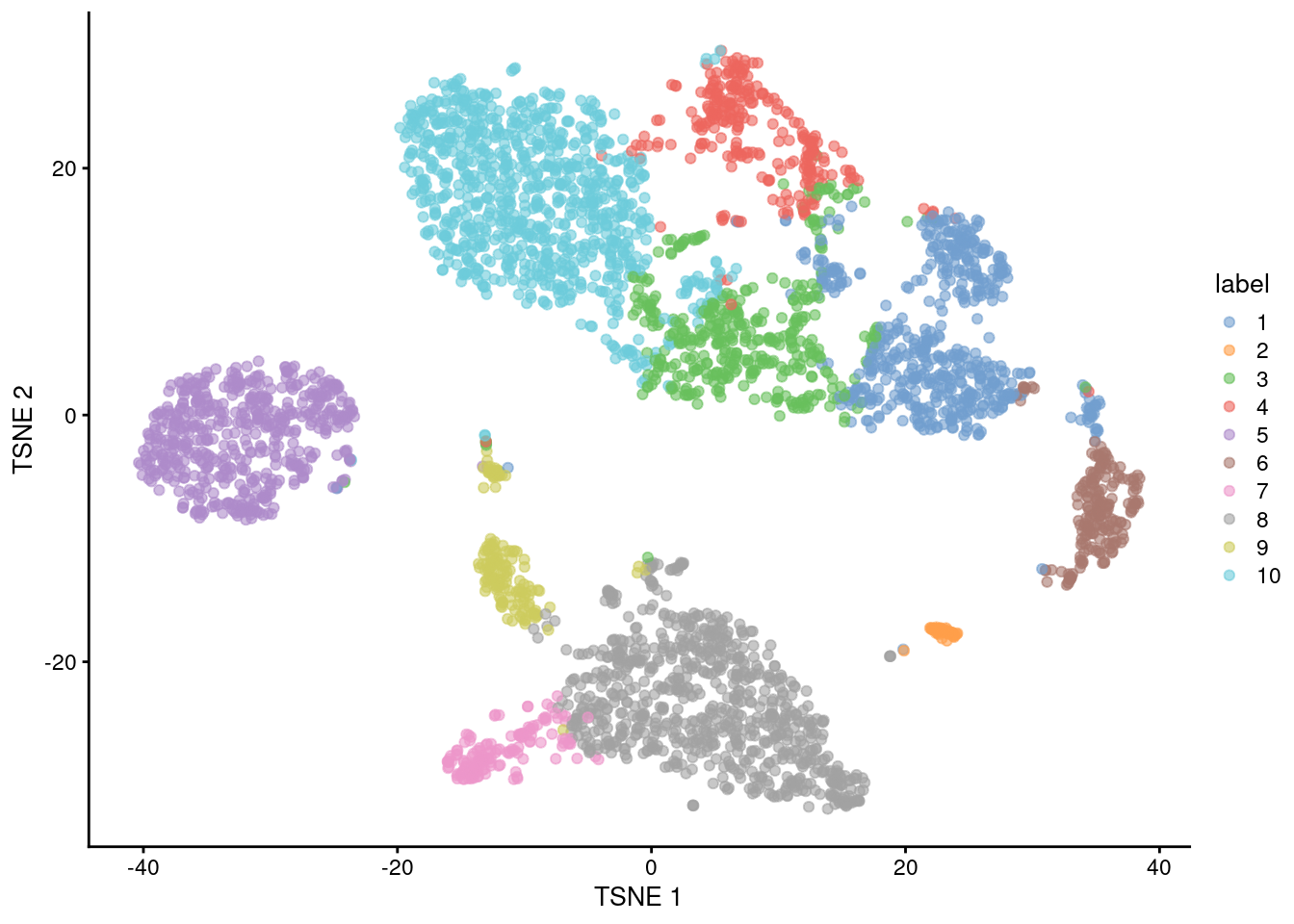
$t$-SNE plot of the 10X PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from $k$-means clustering.

Figure 5.4: \(t\)-SNE plot of the 10X PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from \(k\)-means clustering.

If we were so inclined, we could obtain a “reasonable” choice of \(k\) by computing the gap statistic using methods from the cluster package. A more practical use of \(k\)-means is to deliberately set \(k\) to a large value to achieve overclustering. This will forcibly partition cells inside broad clusters that do not have well-defined internal structure. For example, we might be interested in the change in expression from one “side” of a cluster to the other, but the lack of any clear separation within the cluster makes it difficult to separate with graph-based methods, even at the highest resolution. \(k\)-means has no such problems and will readily split these broad clusters for greater resolution.

## clust.kmeans2
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20 
## 243  28 202 361 282 166 388 150 114 537 170  96  46 131 162 118 201 257 288  45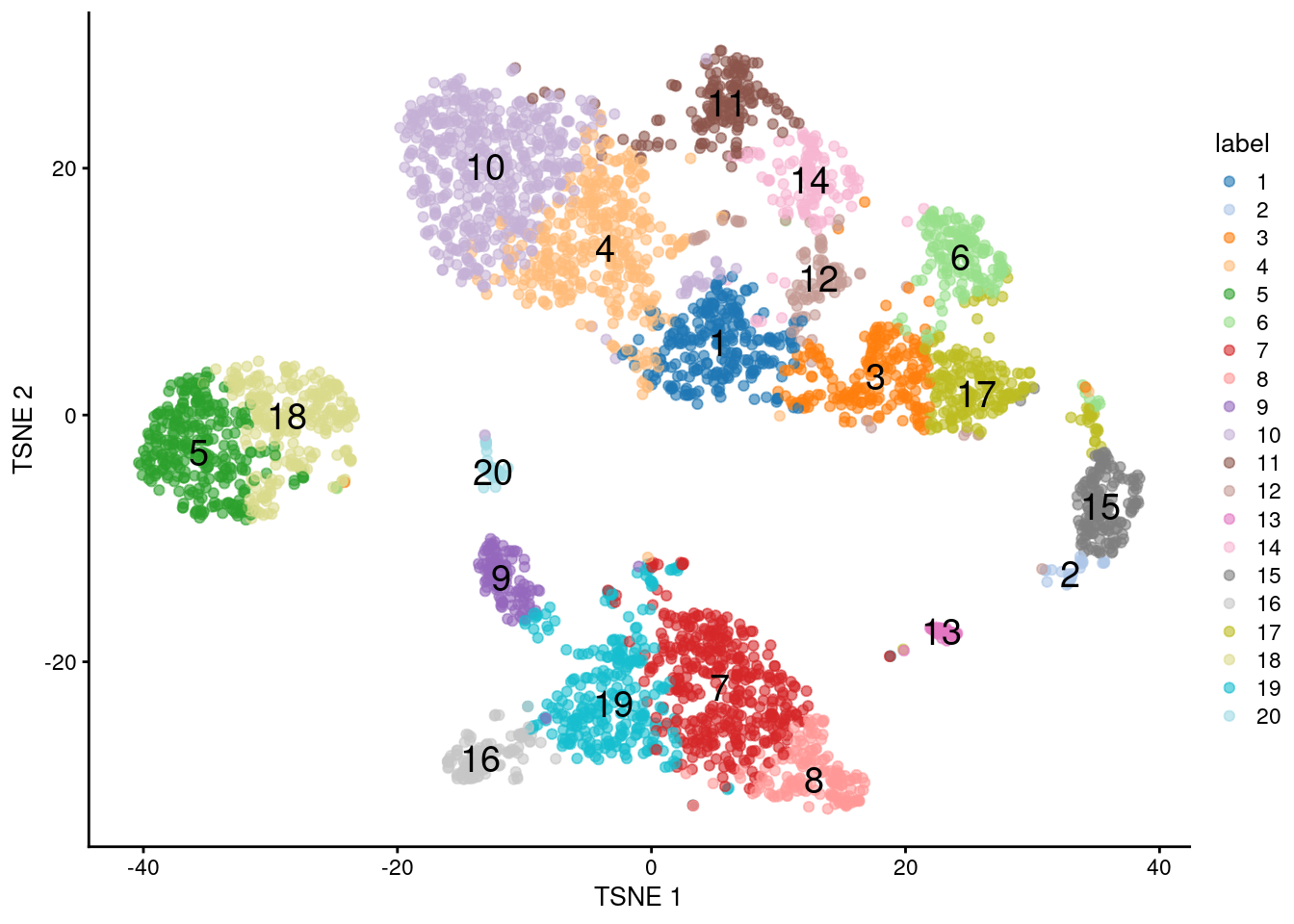
$t$-SNE plot of the 10X PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from $k$-means clustering with $k=20$.

Figure 5.5: \(t\)-SNE plot of the 10X PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from \(k\)-means clustering with \(k=20\).

For larger datasets, we can use a variant of this approach named mini-batch \(k\)-means from the mbkmeans package. At each iteration, we only update the cluster assignments and centroid positions for a small subset of the observations. This reduces memory usage and computational time - especially when not all of the observations are informative for convergence - and supports parallelization via BiocParallel. Using this variant is as simple as switching to a MbkmeansParam() object in our clusterCells() call:

## clust.mbkmeans
##    1    2    3    4    5    6    7    8    9   10 
##  210  158  441  138 1385  709  540  243   46  115

5.3.3 In two-step procedures

By itself, \(k\)-means suffers from several shortcomings that reduce its appeal for obtaining interpretable clusters:

  • It implicitly favors spherical clusters of equal radius. This can lead to unintuitive partitionings on real datasets that contain groupings with irregular sizes and shapes.
  • The number of clusters \(k\) must be specified beforehand and represents a hard cap on the resolution of the clustering.. For example, setting \(k\) to be below the number of cell types will always lead to co-clustering of two cell types, regardless of how well separated they are. In contrast, other methods like graph-based clustering will respect strong separation even if the relevant resolution parameter is set to a low value.
  • It is dependent on the randomly chosen initial coordinates. This requires multiple runs to verify that the clustering is stable.

However, these concerns are less relevant when \(k\)-means is being used for vector quantization. In this application, \(k\)-means is used as a prelude to more sophisticated and interpretable - but computationally expensive - clustering algorithms. The clusterCells() function supports a “two-step” mode where \(k\)-means is initially used to obtain representative centroids that are subjected to graph-based clustering. Each cell is then placed in the same graph-based cluster that its \(k\)-means centroid was assigned to (Figure 5.6).

## kgraph.clusters
##   1   2   3   4   5   6   7   8   9  10  11  12 
## 191 854 506 541 541 892  46 120  29 132  47  86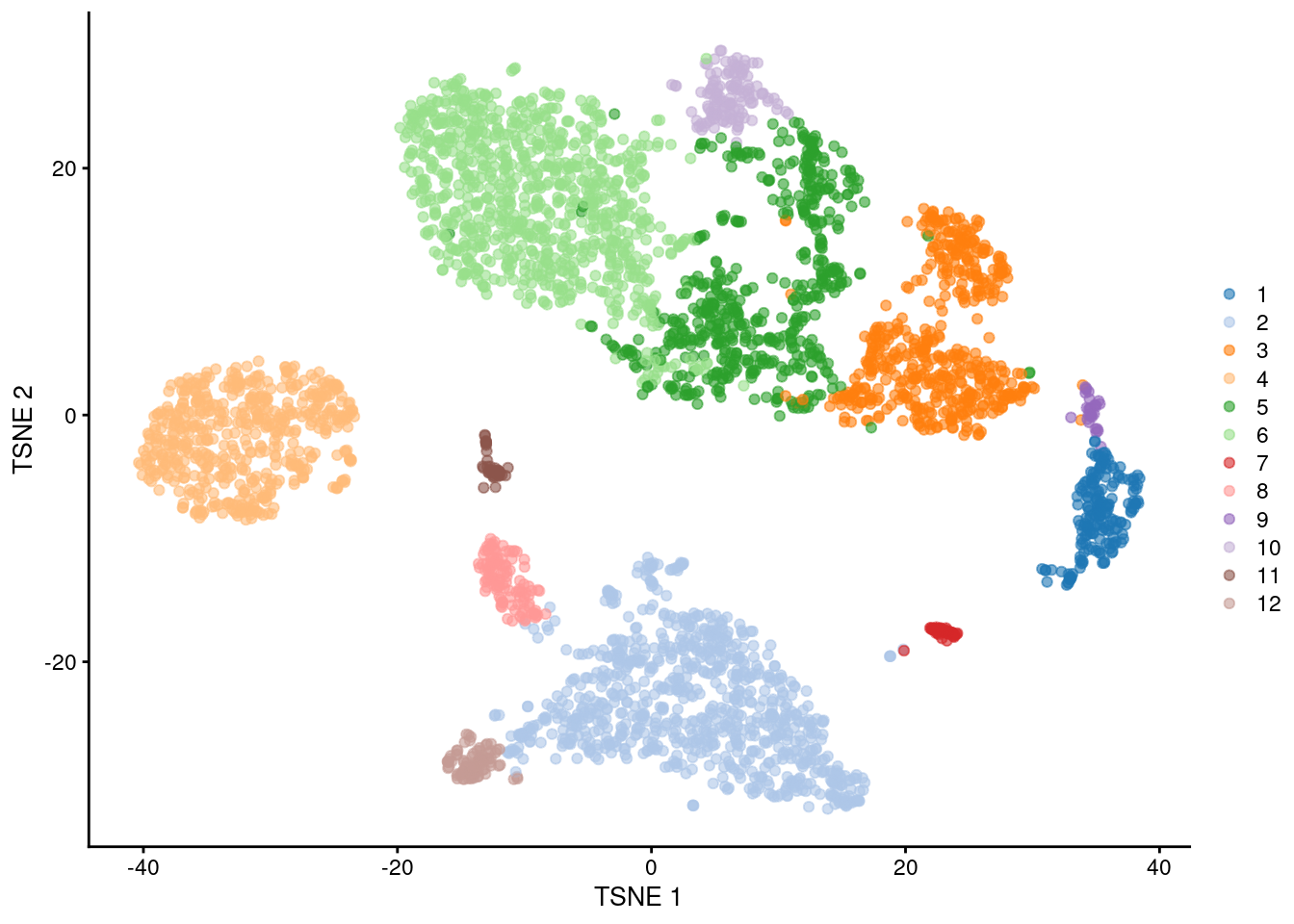
$t$-SNE plot of the PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from combined $k$-means/graph-based clustering.

Figure 5.6: \(t\)-SNE plot of the PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from combined \(k\)-means/graph-based clustering.

The obvious benefit of this approach over direct graph-based clustering is the speed improvement. We avoid the need to identifying nearest neighbors for each cell and the construction of a large intermediate graph, while benefiting from the relative interpretability of graph-based clusters compared to those from \(k\)-means. This approach also mitigates the “inflation” effect discussed in Section 5.2. Each centroid serves as a representative of a region of space that is roughly similar in volume, ameliorating differences in cell density that can cause (potentially undesirable) differences in resolution.

The choice of the number of \(k\)-means clusters determines the trade-off between speed and fidelity. Larger values provide a more faithful representation of the underlying distribution of cells, at the cost of requiring more computational work by the second-step clustering procedure. Note that the second step operates on the centroids, so increasing clusters= may have further implications if the second-stage procedure is sensitive to the total number of input observations. For example, increasing the number of centroids would require an concomitant increase in k= (the number of neighbors in graph construction) to maintain the same level of resolution in the final output.

5.4 Hierarchical clustering

5.4.1 Background

Hierarchical clustering is an old technique that arranges samples into a hierarchy based on their relative similarity to each other. Most implementations do so by joining the most similar samples into a new cluster, then joining similar clusters into larger clusters, and so on, until all samples belong to a single cluster. This process yields obtain a dendrogram that defines clusters with progressively increasing granularity. Variants of hierarchical clustering methods primarily differ in how they choose to perform the agglomerations. For example, complete linkage aims to merge clusters with the smallest maximum distance between their elements, while Ward’s method aims to minimize the increase in within-cluster variance.

In the context of scRNA-seq, the main advantage of hierarchical clustering lies in the production of the dendrogram. This is a rich summary that quantitatively captures the relationships between subpopulations at various resolutions. Cutting the dendrogram at high resolution is also guaranteed to yield clusters that are nested within those obtained at a low-resolution cut; this can be helpful for interpretation, as discussed in Section 5.5. The dendrogram is also a natural representation of the data in situations where cells have descended from a relatively recent common ancestor.

In practice, hierarchical clustering is too slow to be used for anything but the smallest scRNA-seq datasets. Most implementations require a cell-cell distance matrix that is prohibitively expensive to compute for a large number of cells. Greedy agglomeration is also likely to result in a quantitatively suboptimal partitioning (as defined by the agglomeration measure) at higher levels of the dendrogram when the number of cells and merge steps is high. Nonetheless, we will still demonstrate the application of hierarchical clustering here as it can be useful when combined with vector quantization techniques like \(k\)-means.

5.4.2 Implementation

The PBMC dataset is too large to use directly in hierarchical clustering, requiring a two-step approach to compress the observations instead (Section 5.3.3). For the sake of simplicity, we will demonstrate on the smaller 416B dataset instead.

#--- loading ---#
library(scRNAseq)
sce.416b <- LunSpikeInData(which="416b") 
sce.416b$block <- factor(sce.416b$block)

#--- gene-annotation ---#
library(AnnotationHub)
ens.mm.v97 <- AnnotationHub()[["AH73905"]]
rowData(sce.416b)$ENSEMBL <- rownames(sce.416b)
rowData(sce.416b)$SYMBOL <- mapIds(ens.mm.v97, keys=rownames(sce.416b),
    keytype="GENEID", column="SYMBOL")
rowData(sce.416b)$SEQNAME <- mapIds(ens.mm.v97, keys=rownames(sce.416b),
    keytype="GENEID", column="SEQNAME")

library(scater)
rownames(sce.416b) <- uniquifyFeatureNames(rowData(sce.416b)$ENSEMBL, 
    rowData(sce.416b)$SYMBOL)

#--- quality-control ---#
mito <- which(rowData(sce.416b)$SEQNAME=="MT")
stats <- perCellQCMetrics(sce.416b, subsets=list(Mt=mito))
qc <- quickPerCellQC(stats, percent_subsets=c("subsets_Mt_percent",
    "altexps_ERCC_percent"), batch=sce.416b$block)
sce.416b <- sce.416b[,!qc$discard]

#--- normalization ---#
library(scran)
sce.416b <- computeSumFactors(sce.416b)
sce.416b <- logNormCounts(sce.416b)

#--- variance-modelling ---#
dec.416b <- modelGeneVarWithSpikes(sce.416b, "ERCC", block=sce.416b$block)
chosen.hvgs <- getTopHVGs(dec.416b, prop=0.1)

#--- batch-correction ---#
library(limma)
assay(sce.416b, "corrected") <- removeBatchEffect(logcounts(sce.416b), 
    design=model.matrix(~sce.416b$phenotype), batch=sce.416b$block)

#--- dimensionality-reduction ---#
sce.416b <- runPCA(sce.416b, ncomponents=10, subset_row=chosen.hvgs,
    exprs_values="corrected", BSPARAM=BiocSingular::ExactParam())

set.seed(1010)
sce.416b <- runTSNE(sce.416b, dimred="PCA", perplexity=10)
## class: SingleCellExperiment 
## dim: 46604 185 
## metadata(0):
## assays(3): counts logcounts corrected
## rownames(46604): 4933401J01Rik Gm26206 ... CAAA01147332.1
##   CBFB-MYH11-mcherry
## rowData names(4): Length ENSEMBL SYMBOL SEQNAME
## colnames(185): SLX-9555.N701_S502.C89V9ANXX.s_1.r_1
##   SLX-9555.N701_S503.C89V9ANXX.s_1.r_1 ...
##   SLX-11312.N712_S507.H5H5YBBXX.s_8.r_1
##   SLX-11312.N712_S517.H5H5YBBXX.s_8.r_1
## colData names(10): Source Name cell line ... block sizeFactor
## reducedDimNames(2): PCA TSNE
## mainExpName: endogenous
## altExpNames(2): ERCC SIRV

We use a HclustParam object to instruct clusterCells() to perform hierarchical clustering on the top PCs. Specifically, it computes a cell-cell distance matrix using the top PCs and then applies Ward’s minimum variance method to obtain a dendrogram. When visualized in Figure 5.7, we see a clear split in the population caused by oncogene induction. While both Ward’s method and the default complete linkage yield compact clusters, we prefer the former it is less affected by differences in variance between clusters.

Hierarchy of cells in the 416B data set after hierarchical clustering, where each leaf node is a cell that is coloured according to its oncogene induction status (red is induced, blue is control) and plate of origin (light or dark).

Figure 5.7: Hierarchy of cells in the 416B data set after hierarchical clustering, where each leaf node is a cell that is coloured according to its oncogene induction status (red is induced, blue is control) and plate of origin (light or dark).

To obtain explicit clusters, we “cut” the tree by removing internal branches such that every subtree represents a distinct cluster. This is most simply done by removing internal branches above a certain height of the tree, as performed by the cutree() function. A more sophisticated variant of this approach is implemented in the dynamicTreeCut package, which uses the shape of the branches to obtain a better partitioning for complex dendrograms (Figure 5.8). We enable this option by setting cut.dynamic=TRUE, with additional tweaking of the deepSplit= parameter to control the resolution of the resulting clusters.

## hclust.dyn
##  1  2  3  4 
## 78 69 24 14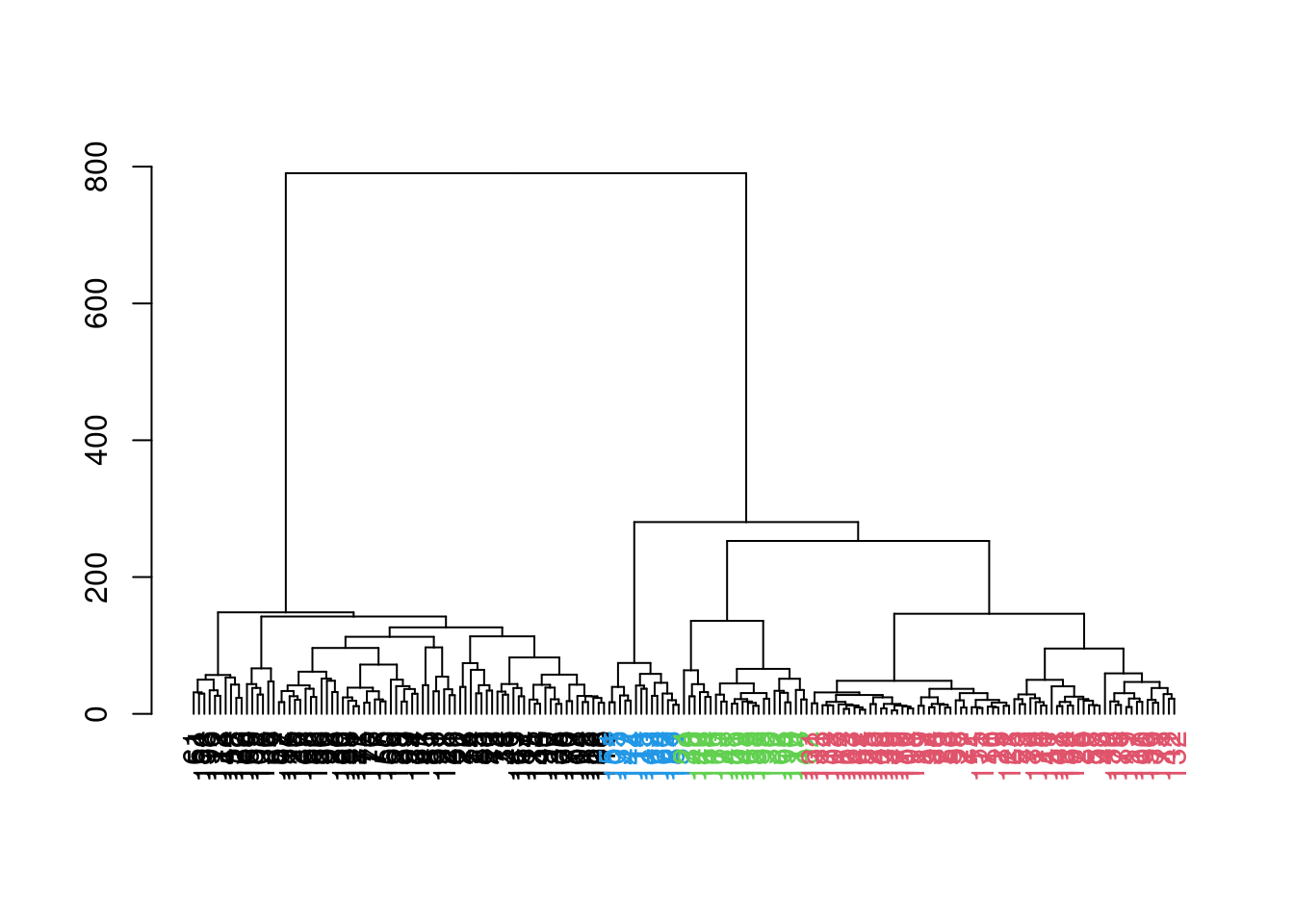
Hierarchy of cells in the 416B data set after hierarchical clustering, where each leaf node is a cell that is coloured according to its assigned cluster identity from a dynamic tree cut.

Figure 5.8: Hierarchy of cells in the 416B data set after hierarchical clustering, where each leaf node is a cell that is coloured according to its assigned cluster identity from a dynamic tree cut.

This generally corresponds well to the grouping of cells on a \(t\)-SNE plot (Figure 5.9). Cluster 2 is split across two visual clusters in the plot but we attribute this to a distortion introduced by \(t\)-SNE, given that this cluster actually has the highest average silhouette width (link("silhouette-width", "OSCA.advanced")).

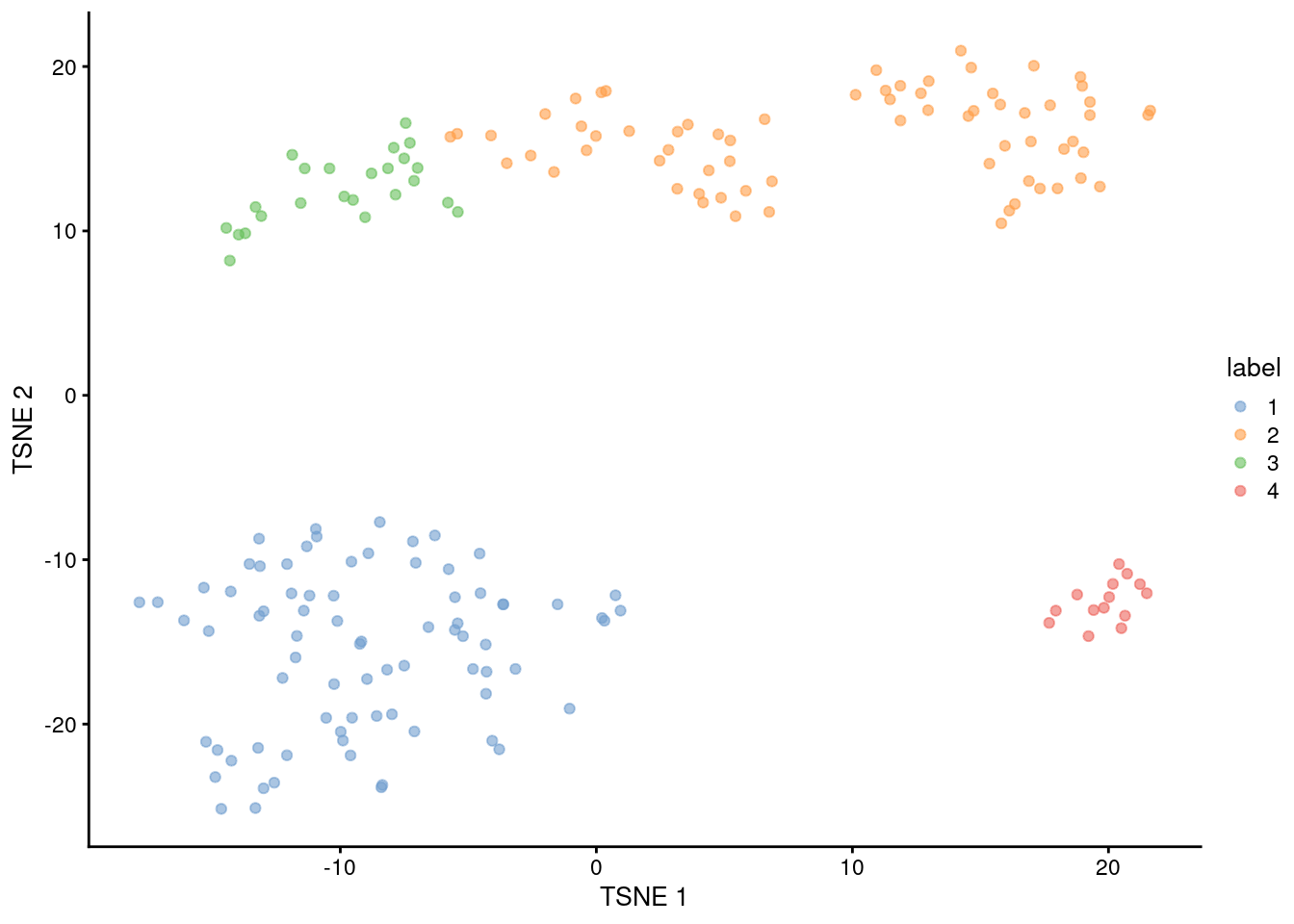
$t$-SNE plot of the 416B dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from hierarchical clustering.

Figure 5.9: \(t\)-SNE plot of the 416B dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from hierarchical clustering.

5.4.3 In two-step procedures, again

Returning to our PBMC example, we can use a two-step approach to perform hierarchical clustering on the representative centroids (Figure 5.10). This avoids the construction of a distance matrix across all cells for faster computation.

## 
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18 
## 649 374 347 328 281 243 218 223 161 157 172 133 135 167  93 117  72 115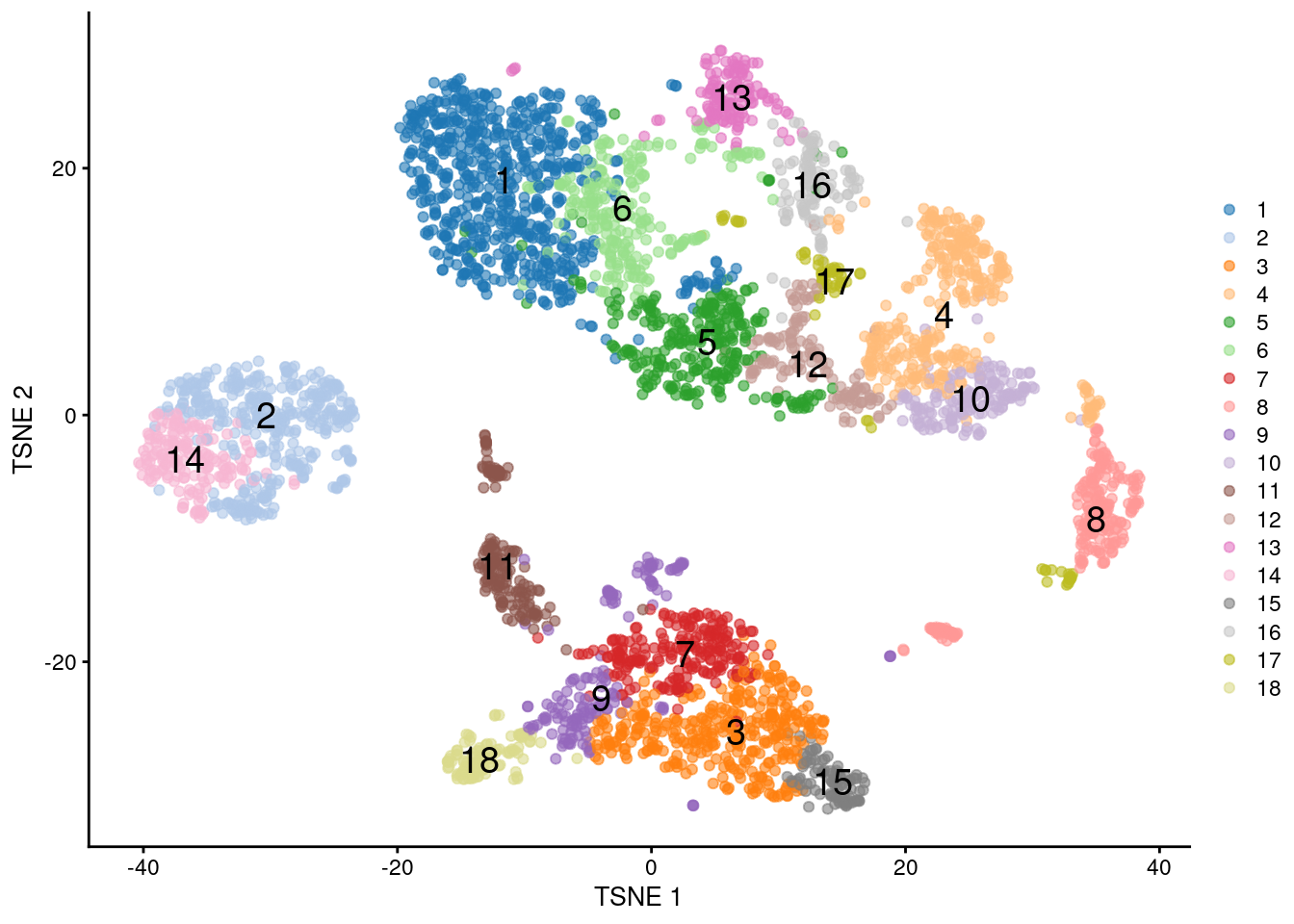
$t$-SNE plot of the PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from combined $k$-means/hierarchical clustering.

Figure 5.10: \(t\)-SNE plot of the PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from combined \(k\)-means/hierarchical clustering.

With a little bit of work, we can also examine the dendrogram constructed on the centroids (Figure 5.11). This provides a more quantitative visualization of the relative similarities between the different subpopulations.

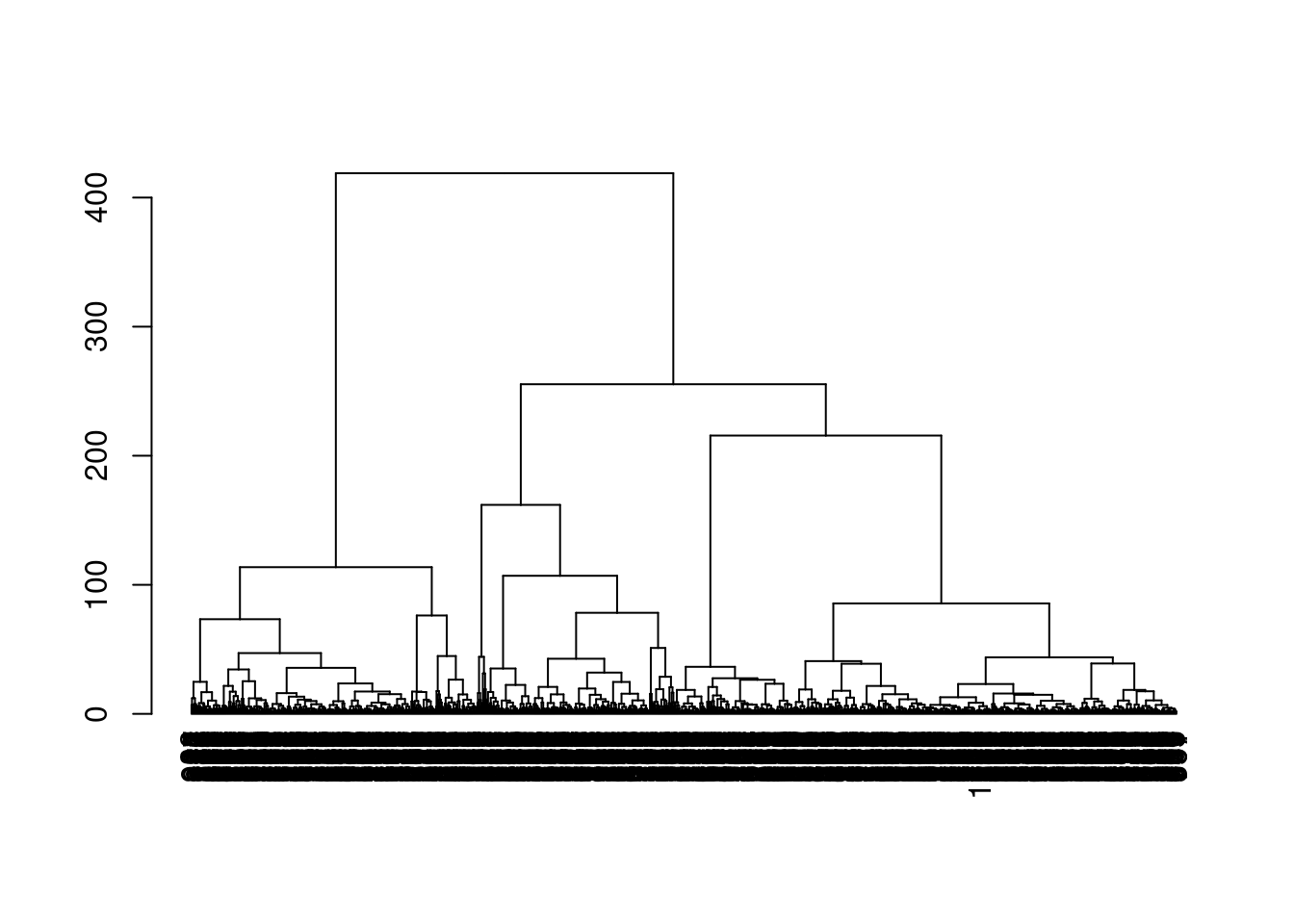
Dendrogram of the $k$-mean centroids after hierarchical clustering in the PBMC dataset. Each leaf node represents a representative cluster of cells generated by $k$-mean clustering.

Figure 5.11: Dendrogram of the \(k\)-mean centroids after hierarchical clustering in the PBMC dataset. Each leaf node represents a representative cluster of cells generated by \(k\)-mean clustering.

As an aside, the same approach can be used to speed up any clustering method based on a distance matrix. For example, we could subject our \(k\)-means centroids to clustering by affinity propagation (Frey and Dueck 2007). In this procedure, each sample (i.e., centroid) chooses itself or another sample as its “exemplar”, with the suitability of the choice dependent on the distance between the samples, other potential exemplars for each sample, and the other samples with the same chosen exemplar. Iterative updates of these choices yields a set of clusters where each cluster is defined from the samples assigned to the same exemplar (Figure 5.12) Unlike hierarchical clustering, this does not provide a dendrogram, but it also avoids the extra complication of a tree cut - resolution is primarily controlled via the q= parameter, which defines the strength with which a sample considers itself as an exemplar and thus forms its own cluster.

## 
##   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18 
## 847 144 392  93 405 264 170 209 379 187  24  20  45 121 536  27  64  58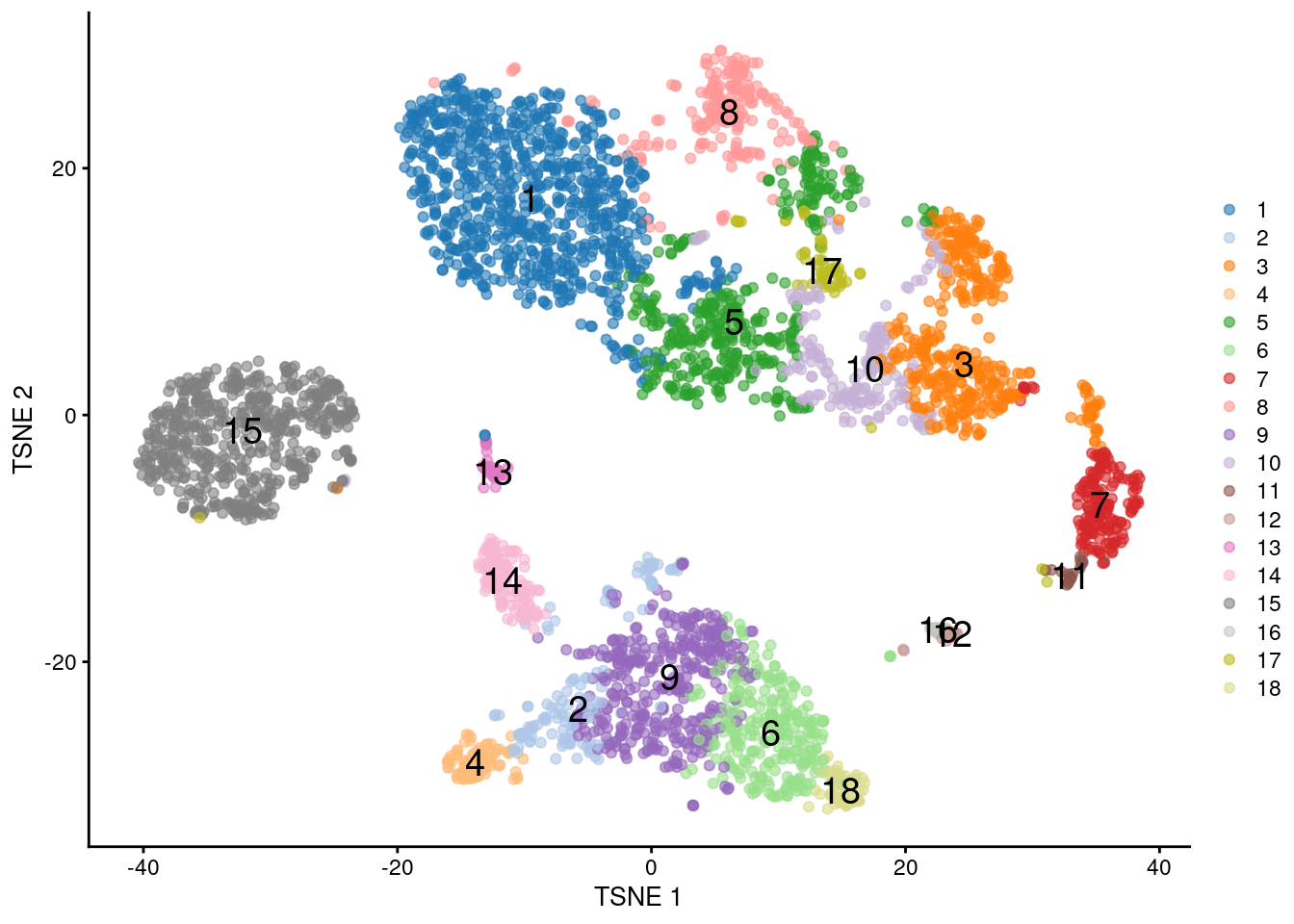
$t$-SNE plot of the PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from combined $k$-means/affinity propagation clustering.

Figure 5.12: \(t\)-SNE plot of the PBMC dataset, where each point represents a cell and is coloured according to the identity of the assigned cluster from combined \(k\)-means/affinity propagation clustering.

5.5 Subclustering

Another simple approach to improving resolution is to repeat the feature selection and clustering within a single cluster. This aims to select HVGs and PCs that are more relevant to internal structure, improving resolution by avoiding noise from unnecessary features. Subsetting also encourages clustering methods to separate cells according to more modest heterogeneity in the absence of distinct subpopulations. We demonstrate with a cluster of putative memory T cells from the PBMC dataset, identified according to several markers (Figure 5.13).

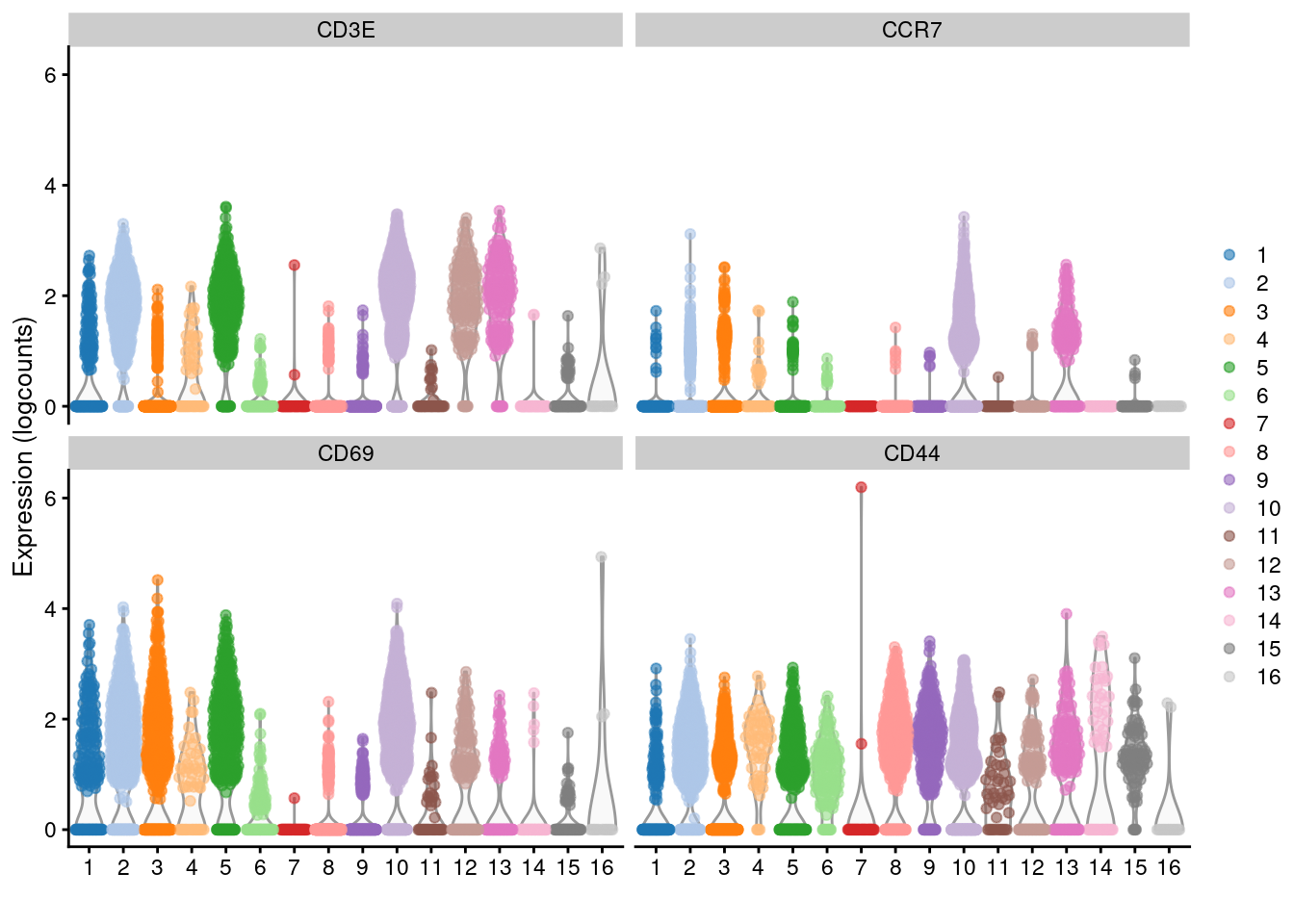
Distribution of log-normalized expression values for several T cell markers within each cluster in the 10X PBMC dataset. Each cluster is color-coded for convenience.

Figure 5.13: Distribution of log-normalized expression values for several T cell markers within each cluster in the 10X PBMC dataset. Each cluster is color-coded for convenience.

We apply graph-based clustering within this memory subset to obtain CD4+ and CD8+ subclusters (Figure 5.14). Admittedly, the expression of CD4 is so low that the change is rather modest, but the interpretation is clear enough.

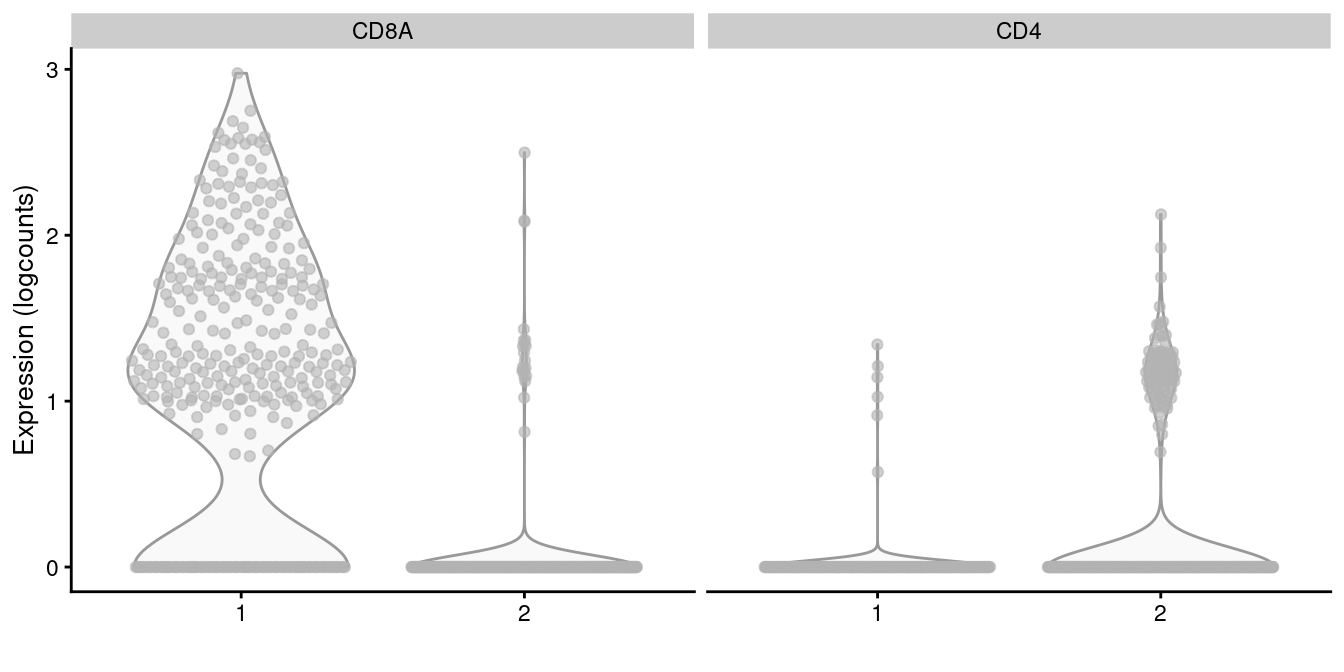
Distribution of _CD4_ and _CD8A_ log-normalized expression values within each cluster in the memory T cell subset of the 10X PBMC dataset.

Figure 5.14: Distribution of CD4 and CD8A log-normalized expression values within each cluster in the memory T cell subset of the 10X PBMC dataset.

For subclustering analyses, it is helpful to define a customized function that calls our desired algorithms to obtain a clustering from a given SingleCellExperiment. This function can then be applied multiple times on different subsets without having to repeatedly copy and modify the code for each subset. For example, quickSubCluster() loops over all subsets and executes this user-specified function to generate a list of SingleCellExperiment objects containing the subclustering results. (Of course, the downside is that this assumes that a similar analysis is appropriate for each subset. If different subsets require extensive reparametrization, copying the code may actually be more straightforward.)

##  [1] "1"  "2"  "3"  "4"  "5"  "6"  "7"  "8"  "9"  "10" "11" "12" "13" "14" "15"
## [16] "16"
## 
## 1.1 1.2 1.3 1.4 1.5 1.6 
##  28  22  34  62  11  48

Subclustering is a general and conceptually straightforward procedure for increasing resolution. It can also simplify the interpretation of the subclusters, which only need to be considered in the context of the parent cluster’s identity - for example, we did not have to re-identify the cells in cluster 10 as T cells. However, this is a double-edged sword as it is difficult for practitioners to consider the uncertainty of identification for parent clusters when working with deep nesting. If cell types or states span cluster boundaries, conditioning on the putative cell type identity of the parent cluster can encourage the construction of a “house of cards” of cell type assignments, e.g., where a subcluster of one parent cluster is actually contamination from a cell type in a separate parent cluster.

Session Info

R version 4.1.0 (2021-05-18)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 20.04.2 LTS

Matrix products: default
BLAS:   /home/biocbuild/bbs-3.13-bioc/R/lib/libRblas.so
LAPACK: /home/biocbuild/bbs-3.13-bioc/R/lib/libRlapack.so

locale:
 [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
 [3] LC_TIME=en_US.UTF-8        LC_COLLATE=C              
 [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
 [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
 [9] LC_ADDRESS=C               LC_TELEPHONE=C            
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       

attached base packages:
[1] parallel  stats4    stats     graphics  grDevices utils     datasets 
[8] methods   base     

other attached packages:
 [1] apcluster_1.4.8             dendextend_1.15.1          
 [3] pheatmap_1.0.12             bluster_1.2.0              
 [5] scater_1.20.0               ggplot2_3.3.3              
 [7] scran_1.20.0                scuttle_1.2.0              
 [9] SingleCellExperiment_1.14.0 SummarizedExperiment_1.22.0
[11] Biobase_2.52.0              GenomicRanges_1.44.0       
[13] GenomeInfoDb_1.28.0         IRanges_2.26.0             
[15] S4Vectors_0.30.0            BiocGenerics_0.38.0        
[17] MatrixGenerics_1.4.0        matrixStats_0.58.0         
[19] BiocStyle_2.20.0            rebook_1.2.0               

loaded via a namespace (and not attached):
 [1] ggbeeswarm_0.6.0          colorspace_2.0-1         
 [3] ellipsis_0.3.2            dynamicTreeCut_1.63-1    
 [5] benchmarkme_1.0.7         XVector_0.32.0           
 [7] BiocNeighbors_1.10.0      farver_2.1.0             
 [9] fansi_0.4.2               ClusterR_1.2.4           
[11] codetools_0.2-18          sparseMatrixStats_1.4.0  
[13] doParallel_1.0.16         knitr_1.33               
[15] jsonlite_1.7.2            cluster_2.1.2            
[17] graph_1.70.0              httr_1.4.2               
[19] BiocManager_1.30.15       compiler_4.1.0           
[21] dqrng_0.3.0               assertthat_0.2.1         
[23] Matrix_1.3-3              limma_3.48.0             
[25] BiocSingular_1.8.0        htmltools_0.5.1.1        
[27] tools_4.1.0               gmp_0.6-2                
[29] rsvd_1.0.5                igraph_1.2.6             
[31] gtable_0.3.0              glue_1.4.2               
[33] GenomeInfoDbData_1.2.6    dplyr_1.0.6              
[35] rappdirs_0.3.3            Rcpp_1.0.6               
[37] jquerylib_0.1.4           vctrs_0.3.8              
[39] iterators_1.0.13          DelayedMatrixStats_1.14.0
[41] xfun_0.23                 stringr_1.4.0            
[43] beachmat_2.8.0            lifecycle_1.0.0          
[45] irlba_2.3.3               gtools_3.8.2             
[47] statmod_1.4.36            XML_3.99-0.6             
[49] edgeR_3.34.0              zlibbioc_1.38.0          
[51] scales_1.1.1              RColorBrewer_1.1-2       
[53] yaml_2.2.1                gridExtra_2.3            
[55] sass_0.4.0                stringi_1.6.2            
[57] highr_0.9                 foreach_1.5.1            
[59] ScaledMatrix_1.0.0        filelock_1.0.2           
[61] BiocParallel_1.26.0       benchmarkmeData_1.0.4    
[63] rlang_0.4.11              pkgconfig_2.0.3          
[65] bitops_1.0-7              evaluate_0.14            
[67] lattice_0.20-44           purrr_0.3.4              
[69] CodeDepends_0.6.5         labeling_0.4.2           
[71] cowplot_1.1.1             tidyselect_1.1.1         
[73] magrittr_2.0.1            bookdown_0.22            
[75] R6_2.5.0                  generics_0.1.0           
[77] metapod_1.0.0             DelayedArray_0.18.0      
[79] DBI_1.1.1                 pillar_1.6.1             
[81] withr_2.4.2               mbkmeans_1.8.0           
[83] RCurl_1.98-1.3            tibble_3.1.2             
[85] dir.expiry_1.0.0          crayon_1.4.1             
[87] utf8_1.2.1                rmarkdown_2.8            
[89] viridis_0.6.1             locfit_1.5-9.4           
[91] grid_4.1.0                digest_0.6.27            
[93] munsell_0.5.0             beeswarm_0.3.1           
[95] viridisLite_0.4.0         vipor_0.4.5              
[97] bslib_0.2.5.1

References

Frey, B. J., and D. Dueck. 2007. “Clustering by passing messages between data points.” Science 315 (5814): 972–76.

Ji, Z., and H. Ji. 2016. “TSCAN: Pseudo-time reconstruction and evaluation in single-cell RNA-seq analysis.” Nucleic Acids Res. 44 (13): e117.

Xu, C., and Z. Su. 2015. “Identification of cell types from single-cell transcriptomes using a novel clustering method.” Bioinformatics 31 (12): 1974–80.

  1. Sten Linarrsson talked about this in SCG2018, but I don’t know where that work ended up. So this is what passes as a reference for the time being.↩